martes, 23 de octubre de 2012
Charla de Gustavo Piñeiro en el encuentro 2012
Caminata marciana
En esta ocasión voy a invitarlos a pasear por Marte... ¿Qué es Marte? "Un planeta" me responderán ustedes, con toda razón. Pero para nosotros el mapa de ese planeta será un cuadriculado ilimitado que sigue infintamente en todas direcciones.
Un camino en ese cuadriculado será cualquier recorrido que comience en una casilla y termine en otra (todos nuestros caminos tendrán un comienzo y un final, ninguno seguirá indefinidamente), que pase de cada casilla a otra que sea vecina en horizontal, vertical o diagonal, y que nunca pase dos veces por la misma casilla.
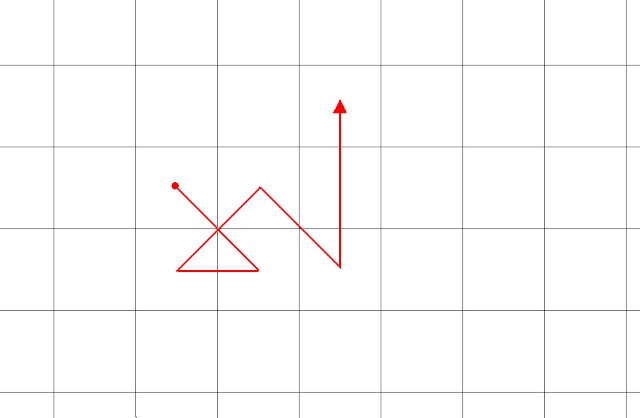
En la siguiente figura vemos un ejemplo de camino (el circulito rojo indica su comienzo y la flecha indica el final).
Una vez que hemos dibujado el camino, en las casillas visitadas por él (y sólo en esas) vamos a colocar números. Los números serán colocados en el mismo orden en que las casillas fueron visitadas por el camino y de acuerdo con la siguiente regla: en cada casilla va el número que indica la cantidad de números que, hasta ese momento, hay alrededor de la casilla.
En el ejemplo anterior, la primera casilla (la del circulito) no tiene todavía número alrededor, de modo que allí va un 0 (la primera casilla siempre tendrá un 0).
La siguiente casilla tiene ahora un número a su alrededor (el 0 que acabamos de poner), de modo que en la segunda casilla va un 1. La siguiente tendrá un 2, y así sucesivamente. El camino, con todos los números colocados se ve así:
Éste es el mecanismo básico: dibujamos un camino y colocamos los números según la regla que acabamos de enunciar. A partir de este mecanismo podemos plantear una serie de desafíos.
Desafío 1: Dibujar un camino en el que aparezcan, al menos una vez, todos los números del 0 al 8 (es claro que el mayor número que puede aparecer es el 8).
Un ejemplo es el siguiente:
Que, al colocar los números, se ve así (he marcado en amarillo los números del 0 al 8 para que se destaquen).
Como se ve, hay muchos números adicionales (todos los que quedaron en blanco). El verdadero desafío es logar que la suma de esos números adicionales sea la mínima posible.
Desafío 1 (completo): Dibujar un camino en el que aparezcan, al menos una vez, todos los números del 0 al 8 de modo tal que la suma de los números adicionales sea la mínima posible. En el ejemplo anterior la suma es 36, esa solución puede mejorarse.
Desafío 2: Dibujar un camino en el que se forme la siguiente distribución de números, de modo tal que la suma de los números adicionales sea la mínima posible.
El interés de esta disposición de números consiste en que se trata de un cuadrado mágico: las tres filas, las tres columna y las dos diagonales suman 12.
Desafío 3 (cráteres): Un cráter es el borde de un cuadrado de n x n con sus casillas (sólo las casillas del borde) ocupadas por números todos iguales entre sí. Por ejemplo, el siguiente es un cráter de 4 x 4 con 3's:
Como antes, el objetivo es encontrar un camino que forme diferentes cráteres de modo tal que la suma de los números adicionales sea la mínima posible. Algunas marcas que he obtenido son las siguientes:
Cráter de 3 x 3 con 2's: es imposible, es decir, no existe un camino que pueda formar un cráter así. A quienes les interese los desafíos de este tipo, pueden intentar demostrar esta imposibilidad.
Cráter de 3 x 3 con 3's: mi mejor solución alcanza una suma de 11 (en un mensaje privado Rodolfo Kurchan, organizador del encuentro, me ha informado que encontró una solución de suma 8, pero no tengo el dibujo de su camino).
Cráter de 3 x 3 con 4's: mi mejor solución alcanza una suma de 9 (en el mismo mensaje privado Rodolfo Kurchan me ha informado que encontró una solución de suma 8, pero tampoco tengo el dibujo de ese camino).
Cráter de 3 x 3 con 5's: mi mejor solución alcanza una suma de 18 (en su mensaje privado Rodolfo Kurchan me ha informado que encontró una solución de suma 15, pero tampoco tengo el dibujo de ese camino).
Cráter de 3 x 3 con 6's: es imposible, como dije antes, quienes estén interesados por desafíos de este tipo pueden intentar demostrar esta imposibilidad.
Cráteres de otros tamaños: el campo está virgen para la exploración.
Existen otras disposiciones interesantes de números que también pueden plantearse como desafíos, pero lo haré más adelante, en otras entradas de este blog.
Quienes encuentren soluciones que quieran transmitir, o nuevos desafíos para plantear a partir de este mecanismo, pueden hacerlo en los comentarios de este enlace. Una manera de de escribir una solución sin recurrir a un dibujo sería indicar las direcciones en que el camino se va desplazando (N = norte o arriba, NO = noroeste, O = oeste o izquierda, etc.) Desde luego, no es relevante la posición de la casilla inicial. Por ejemplo, el camino del primer ejemplo se escribiría así: SE, O, NE, SE, N, N.
Muchas gracias.
Nota: Después de haber preparado esta charla, googleando en busca de ideas similares que alguien hubiera podido tener previamente, descubrí en este enlace un mecanismo más o menos similar, aunque no igual, al que he contado aquí. Como se puede ver en el enlace, también se parte de un camino en el que se escriben números, pero en este otro caso, se pone (un poco arbitrariamente) primero un número 1 y luego se van sumando los números que quedan alrededor. Los desafíos, además, son diferentes. No obstante las diferencias, me pareció correcto mencionar la similitud de ideas.







.bmp)